Index

索引是表中数据的一些属性的备份，它们用来加速查找

DBMS 的取舍：

每个数据库上创建的索引数量

1. 索引存储带来的开销
2. 维护索引带来的开销

B+Tree

诸多数据库采用的索引结构—B+Tree

1. 自平衡树
2. 数据有序（叶子节点）
3. 搜索，线性访问，插入，删除：$O(logn)$

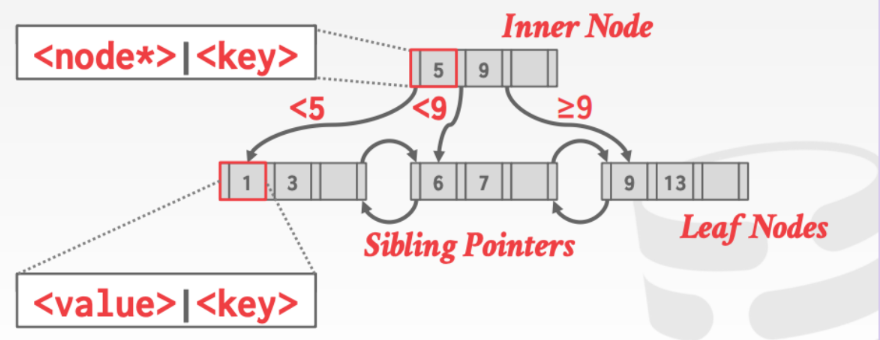
由上图观察可知

1. B+Tree 非常平衡，每个叶子节点到根的距离都是$logN$
2. 每一个节点都至少装了一半以上的元素：M/2 - 1 ≤ #keys ≤ M - 1
3. 每一个有k个key的节点都可以有K+1个子节点，这个理解就是k个节点把数集划分成k+1段，然后根据到来的节点其值大小决定其插入位置。
4. 注意最底层是双向有序链表连接，意味着范围查询比较高效。最底层是有序的key 映射到value

存叶子节点里值的方式

1. record id 存的是指向tuple地址的指针 例如：PostgreSQL Oracle
2. Tuple Data 存的已经是真实的数据 例如：Oracle MySQL

聚簇索引

​ 要求数据在物理上的存储顺序与索引里的顺序一致，这样对于range查找非常有效

B+Tree 的设计策略

Node的大小

当存储器越慢的时候，node的大小应该尽可能的大。原因：当Node比较小的时候，就不得不需要很多层的Innner Nodes，因此就需要更多的遍历层次数，而存储器非常慢，因此我们要避免这种情况，这样树就会尽可能的矮，然后就可以尽可能快的找到数据

Merge Threshold

当插入或者删除时，会破坏Node的定义要求，为了维护这种要求，会进行页Merge。

假如现在就处在这种临界的范围，一次操作会造成页分裂，随后一次操作会造成页合并。显然，如果马上进行上述操作性能是低效的，因此需要推迟它们执行的时间，就引入了merge门限值这个概念。在达到门限值之前，允许这棵树不是严格平衡的。然后引入一个后台垃圾回收器做rebalance，或者干脆周期性的重建树。

变长的Key

业界常用的实现方法：

1. Pointers ，key存的不是真实的data，而是指向data的指针
2. 变长的node长度 ， 变长的长度意味着不统一，需要其它的处理方式
3. Padding，对变长的node进行填充，填充到一致。空间 浪费
4. Key map/ indirection

Non-Unique Indexes

假如index中出现了重复该怎么办？

从叶子节点的角度来看：

1. duplicate keys 重复key 重复value 实践中用的较多
2. value lists key不重复，key指向一串value

从整棵树的角度来看：

1. 把记录ID也当作key的一部分，让key不那么重复
2. 在原来的页后加入溢出页, 但是这与B+Tree的设计初衷相违背

在树中的查找

1. linear 暴力扫描一遍所有的key，显然这是十分低效的
2. Binary Search leafNode已经有序，但是需要维护有序性 最常使用
3. interPolation 比较玄学，通过一些方法模拟出一个offset，然后让你从这个offset开始往后读。

在真实系统中让B+树更快的方式

1. Prefix Compression 前缀压缩，相同的前缀压缩到一个节点，让查找更短 这里用Trie可以更压缩
2. Suffix Truncation 将在查找中用不到后缀截断，让树更矮，查找更快
3. Bulk insert 自底向上建立B+树
4. Pointer Swizzling 通过使用指针的方式来减少对Buffer Pool的查询

隐式索引

大多数的DBMS会给PrimaryKey 自动创建索引

对于其它字段想要为其创建索引的话，需要添加unique关键词

部分索引（Partial Index）

有些时候并不希望为所有的Tuple创建索引，只为其中的一部分创建索引。

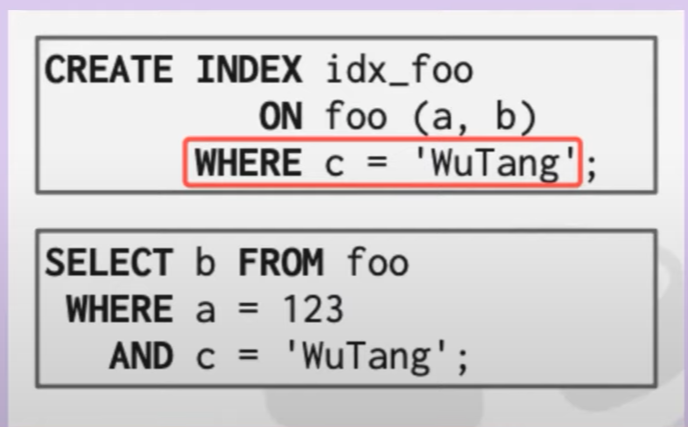
覆盖索引

Index可以cover住所有select的信息

Index include columns

需要查询满足条件a与c的b，假如现在已经有索引ab，但是又不想让c变成索引的一部分，更不希望取所有的tuple中寻找。这时可以在index

中使用include将c这个字段嵌入到index中，此时就成了覆盖索引

Trie Index

前面的B+树实现的索引，想要查找一个不存在的key比较没效率，每一个查询都要查到最底层叶子节点，才能判断是否含有这个数据，这是比较低效的。因此，就有了提前结束查询的方式–Trie

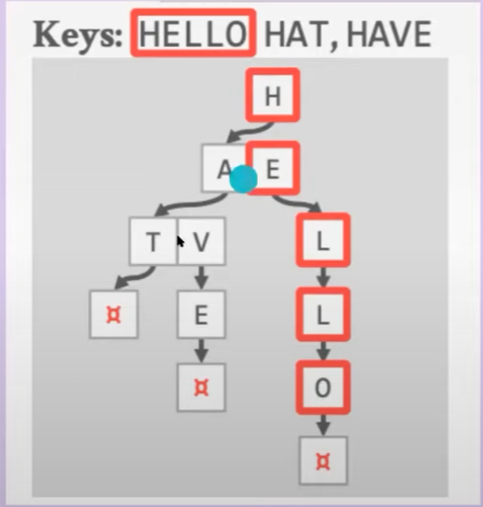
把key拆解成标识，并且key之间也可以公用一部分前缀，节省空间

缺点：key不是存到一块的，当线性扫描时，需要多次回退，性能不如B+树

Inverted index(full-text search index)

希望从文本中找出一个单独的词语，很显然不能把这个文本全部作为索引。例如搜索引擎就是一个很好的例子

于是倒排索引应运而生了，它维护了一个word出现在了哪些地方的记录。